In this article, we will consider several useful and efficient algorithms for an elliptic curve E over a field GF(p) given by the short Weierstrass equation
у^2 = х^3 + Ах + В
- Algorithm for generating a point on curve E
- Algorithm for adding points
- Doubling Point Algorithm
- Algorithm for finding an integer multiple point
- Algorithm for finding an integer multiple point (scalar multiplication)
- Algorithm for constructing a divisor D over a curve E with support supp(D) of a given size d
- Miller’s algorithm for calculating the value of the Weyl function f n, P from a divisor D such that supp(D) ∩ {P, O} = ∅
- Pairing Weil
Modular operations (integers) on a finite field (or Galois field)
- x mod n means “the remainder of n after dividing x”. In other words, if x = an + b and a, b ∈ integer, and also 0 ≤ b ≤ n − 1, then x mod n = b .
- Reverse : if ax = 1 mod n , then a is the reciprocal of x mod n . There are two popular solution methods : • Method 1 : Try each value for a < n as long as xa mod n = 1 .• Method 2 : Euclidean method which is usually used to solve the inverse problem of large integers, so it is recommended to use method 1 to solve inverse problem of small integers.
Elliptic Curve Point Operation
The point P(x 0 , y 0 ) on the elliptic curve E means: its coordinates x 0 and y 0 are elements of the field, and the coordinates x 0 and y 0 satisfy the equation.
- Adding points on an elliptic curve : Let P, Q and R be three points on an elliptic curve. Adding points P + Q = R.
- Doubling points on an elliptic curve : Let P, Q be two points on an elliptic curve. Doubling Points P + P = 2P = Q
- Dot multiplication : let P be a point on the curve E , defined in the equation
- Dot multiplication nP is defined as nP = P + P + P + … + P ( n times), where n is an integer; nP is also a point on the same E curve .
- The minimal natural number a with aP = O is called the order of P .
- Dot multiplication is widely required in elliptic curve cryptosystems.
Divider
Divisor (Divisor) D on a curve E is a convenient way to denote a multiset of points on E , written as a formal sum
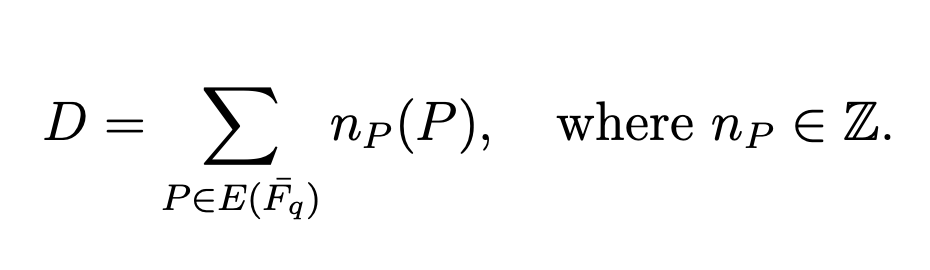
- The set of all divisors on E is denoted by Div F q (E) and forms a group in which the addition of divisors is natural.
- Zero Divisor: This is the divisor for all n P = 0, the zero divisor is 0 ∈ Div F q (E) .
- If the field F q is not specific, it can be omitted and simply written as Div(E) to denote the divisor group.
Function f divided by E
The divisor of a function f by E is used to denote the intersection points (and their multiplicities) of the functions f and E .
Pairing Weil
The Weil pairing, which is denoted by e m , takes as input a pair of points P, Q ∈ E[m] and produces as output a root _m of unity e m ( P , Q) . The bilinearity of the Weyl pairing is expressed by the equations
e m (P 1 + P 2 , Q) \u003d e m (P 1 , Q) * e m (P2, B),
e m (P, Q 1 + Q 2 ) = e m (P, Q 1 ) * e m (P, Q 2 ).
The Weil pair P and Q is the number
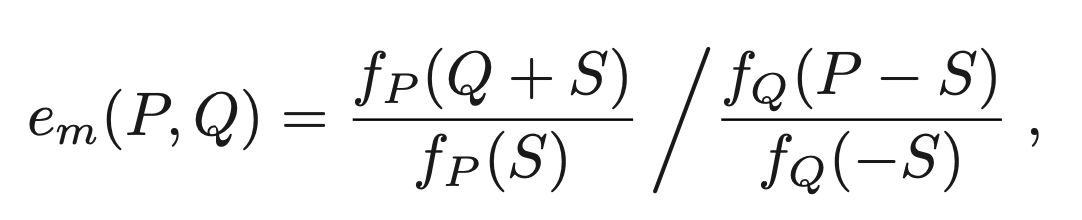
where S ∈ E is any point satisfying the condition S ∉ {O, P, −Q, P − Q} . (This ensures that all quantities on the right hand side are defined and non-zero.) One can check that the value of e m (P,Q) does not depend on the choice of f P , f Q and S .
An Efficient Weil Pairing Computation Algorithm
Let E be an elliptic curve and let P = (x P ,y P ) and Q = (x Q , y Q ) be nonzero points on E .
Let λ be the slope of the line connecting P and Q , or the slope of the tangent to E at P if P = Q. (If the line is vertical, we set λ = ∞.) Define a function g P, Q on E as follows:

then
div(g P, Q ) = [P] + [Q] – [P + Q] – [ O ].
Miller’s algorithm
Let m ≥ and write the binary extension of m as
m \u003d m 0 + m 1 * 2 + m 2 * 2 2 + + m n – 1 2 n – 1
for m i ∈ {0, 1} and m n — 1 ≠ 0 . The following algorithm returns a function f P whose divisor satisfies the condition
div( f P ) = m [ P ] – [ mP ] – ( m – 1 ) [ O ],
where the functions g T, T and g T, P used by the algorithm are defined in (a).

In particular, if P ∈ E[m] , then div( f P ) = m [ P ] − m [ O ].
Requirement
Python 3.5numpy
git clone https://github.com/demining/CryptoDeepTools.git
cd CryptoDeepTools/04AlgorithmsForSecp256k/
pip3 install numpy├── Curves.py <- Набор данных эллиптических кривых
├── Divisor.py <- Создать делитель
├── EllipticCurve.py <- Классы эллиптической кривой и точки на эллиптической кривой
├── EuclideanAlg.py <- Расширенный алгоритм Евклида
├── Helper.py <- Вспомогательные функции (обратные биты, мощность по модулю)
├── Pairing.py <- Спаривания Вейля, а так же Алгоритм Миллера
├── Tests.py <- Модульные тесты для функций
├── Tonelli_ShanksAlg.py <- Алгоритм Тонелли – Шенкса
├── main.py <- main
Telegram: https://t.me/cryptodeeptech
Video: https://youtu.be/gFbiBCNPsFk
