In this article, we will look secp256k1 at the endomorphism acceleration function that helps in optimizing the validation ECDSA for the Bitcoin cryptocurrency, but first, a little history.
12 января 2009 годаSatoshi Nakamoto sent Hal Finney in the earliest bitcoin transactions10 BTC.
That Satoshi Nakamoto chose Hal as the first recipient of Bitcoins is not surprising. Satoshi had great respect for Hal, who established himself as one of the world’s brightest programmers and cryptographers by developing the PGP encryption system . Hal also laid an important foundation for the reusable proof-of-work that Satoshi would use in the development of Bitcoin.
Being one of the best cryptographers in the world, Hal realized that Bitcoin was a huge breakthrough immediately after he stumbled upon it.
Back in it, 2008 году he called Bitcoin “a very promising idea . ”
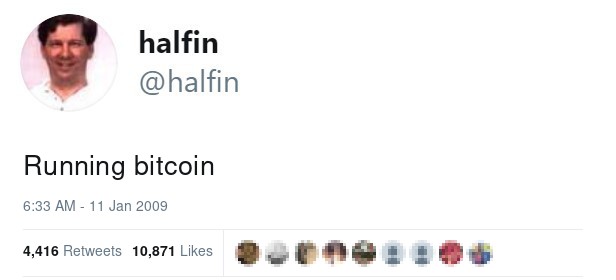
This tweet , posted by
11 января 2009 года, is proof enough that Hal predicted the success of Bitcoin before many even knew what it was.
Two years have passed and 2011 году Hal Finney as a developer and Bitcoin enthusiast wrote on the Bitcointalk forum that the secp256k1 endomorphism function can be used to speed up ECDSA signature verification
LAMBDA and BETA are the values on the secp256k1 curve, where:
secp256k1 uses the following prime number for its x and y coordinates:
p = 0xffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffc2fand the order of the curve:
n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141The first step is to calculate the values of LAMBDA and BETA, such that for any point on the curve Q = (x, y):
LAMBDA * Q = (BETA*х mod р, у)This is the so-called effectively computable endomorphism , and it means that you can multiply any point on the curve
secp256k1by this special value very quickly byLAMBDAdoing a single multiplicationmod p.
The meaning found and published by Hal Finney:
LAMBDA = 0x5363ad4cc05c30e0a5261c028812645a122e22ea20816678df02967c1b23bd72
BETA = 0x7ae96a2b657c07106e64479eac3434e99cf0497512f58995c1396c28719501eeGiven that we can quickly multiply, the LAMBDA, trick is to calculate kQ. Let’s use the calculation first . Then you need to break it into two parts and , each about half the width of , so that: Q' = lambdaQkk1k2n
k = k1 + k2*LAMBDA mod nthen
k*Q = (k1 + k2*LAMBDA)*Q = k1*Q + k2*LAMBDA*Q = k1*Q + k2*Q'This last expression can be computed efficiently using the double multiplication algorithm, and since k1 and k2 are half the length, we get a speedup.
The missing part splits k into k1 and k2. The following 4 values are used for this :
а1 = 0x3086d221a7d46bcde86c90e49284eb15
b1 = -0xe4437ed6010e88286f547fa90abfe4c3
а2 = 0x114ca50f7a8e2f3f657c1108d9d44cfd8
b2 = 0x3086d221a7d46bcde86c90e49284eb15(it’s ok that a1 = b2)
We use them as follows to divide k:
c1 = RoundToNearestInteger(b2*k/n)
c2 = RoundToNearestInteger(-b1*k/n)
k1 = k - c1*a1 - c2*a2
k2 = -c1*b1 - c2*b2We end up with roughly
20%-еa speedup due to the halving of the number of doublings.
This gives many algorithms that can be grouped on multiple points the performance they would have with twice the number of public keys.
This speedup at an equivalent level of optimization makes itsecp256k1the fastest curve to test out of all the commonly used curves.
We learned about the existence of endomorphism in a more detailed study of the repository from the developer and researcher Jean Luc Pons

We previously published an article: “Pollard’s Kangaroo find solutions to the discrete logarithm of secp256k1 PRIVATE KEY + NONCES in a known range” , where we used the source code to build Kangaroo by Jean Luc Pons .
Based on accelerated mechanism Jean Luc Pons pointed VanitySearch
Open main.cpp
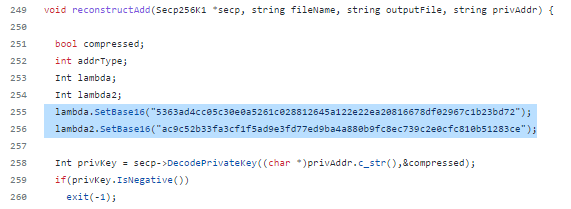
In lines 255 and 256 we see that Jean Luc Pons applied the elliptic curve acceleration function secp256k1 using endomorphism .
lambda.SetBase16("5363ad4cc05c30e0a5261c028812645a122e22ea20816678df02967c1b23bd72");
lambda2.SetBase16("ac9c52b33fa3cf1f5ad9e3fd77ed9ba4a880b9fc8ec739c2e0cfc810b51283ce");Let’s move on to the experimental part:

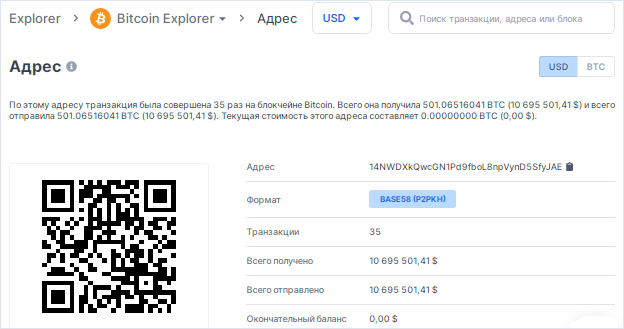
As we remember from the article, we analyzed transactions of Bitcoin Address 14NWDXkQwcGN1Pd9fboL8npVynD5SfyJAE
from the Bitcoin Rich List for a total of more than 10 million US dollars , take this Bitcoin Address as an example
Open Google Colab [TerminalGoogleColab] in the terminal and use the repository “07EndomorphismSecp256k1”
git clone https://github.com/demining/CryptoDeepTools.git
cd CryptoDeepTools/07EndomorphismSecp256k1/
pip3 install base58
Open code endomorphism.py on line 145 we use all short values to speed up secp256k1 with endomorphism
def split_scalar_endo(k):
n = N
a1 = 0x3086d221a7d46bcde86c90e49284eb15
b1 = -0xe4437ed6010e88286f547fa90abfe4c3
a2 = 0x114ca50f7a8e2f3f657c1108d9d44cfd8
b2 = a1
c1 = div_nearest(b2 * k, n)
c2 = div_nearest(-b1 * k, n)
k1 = mod(k - c1 * a1 - c2 * a2, n)
k2 = mod(-c1 * b1 - c2 * b2, n)
k1neg = k1 > POW_2_128
k2neg = k2 > POW_2_128
if k1neg:
k1 = n - k1
if k2neg:
k2 = n - k2
return (k1neg, k1, k2neg, k2)Copy the private key in the HEX-format that we published in the article
HEX: 23d4a09295be678b21a5f1dceae1f634a69c1b41775f680ebf8165266471401bLet’s run the Python script endomorphism.py specifying the private key:
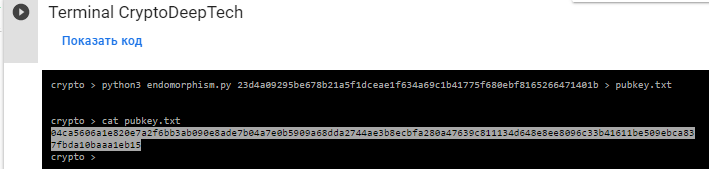
python3 endomorphism.py 23d4a09295be678b21a5f1dceae1f634a69c1b41775f680ebf8165266471401b > pubkey.txt

The result of the public key will be saved to the file: pubkey.txt
Откроем файл: pubkey.txt и проверим:
cat pubkey.txt
04ca5606a1e820e7a2f6bb3ab090e8ade7b04a7e0b5909a68dda2744ae3b8ecbfa280a47639c811134d648e8ee8096c33b41611be509ebca837fbda10baaa1eb15
Next, get the Bitcoin Address by running the Python script pubtoaddr.py
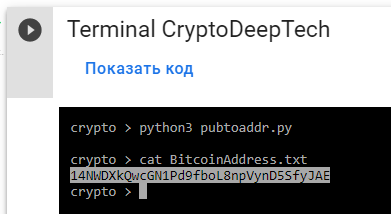
python3 pubtoaddr.py
Откроем файл: BitcoinAddress.txt и проверим:
cat BitcoinAddress.txt
14NWDXkQwcGN1Pd9fboL8npVynD5SfyJAE
ADDR: 14NWDXkQwcGN1Pd9fboL8npVynD5SfyJAE
WIF: 5J64pq77XjeacCezwmAr2V1s7snvvJkuAz8sENxw7xCkikceV6e
HEX: 23d4a09295be678b21a5f1dceae1f634a69c1b41775f680ebf8165266471401b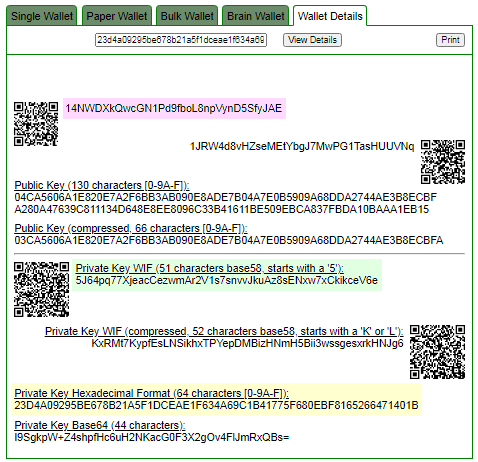
blockchain:
On this topic, you can read the literature:
- Gallant, Robert P., Robert J. Lambert, and Scott A. Wanston. “Faster point multiplication on elliptic curves with efficient endomorphisms” . Annual International Conference on Cryptology, pp. 190–200. Springer, Berlin, Heidelberg, (2001)
- Hankerson, Darrell, Alfred J. Menezes, and Scott Wanston. “A Guide to Elliptic Curve Cryptography” . Computer Reviews 46, no. 1 (2005)
- Hal Finney. bitcointalk – “Acceleration of signature verification” . (2011) https://bitcointalk.org/index.php?topic=3238.0
- Blahut, Richard E. “Cryptography and Secure Communication” . Cambridge University Press, (2014)
This video was created for the CRYPTO DEEP TECH portal to ensure the financial security of data and cryptography on elliptic curves secp256k1 against weak signatures ECDSA in cryptocurrency BITCOIN
Telegram : https://t.me/cryptodeeptech
